Next Page: 4/2 – Meanings of All 53 Notes
*Advanced*
Diagramming Scales
To summarize the basics of the WWMW terms, then, let’s use the example of E1b one circle inside of the central circle. The descriptors for that note surround the intersection of the two lines. Top left: the note in its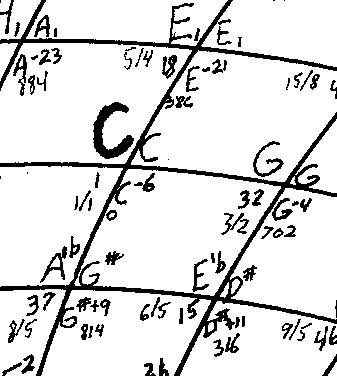 
harmonic context relative to C. Top right: D#, the note you strike on the five-rank keyboard to get the pitch you want. Bottom left: 6/5, the harmonic ratio from C to E1b (ratios appear only on notes close enough to C to have harmonic meaning). Also, the number 15, which means its step number is 15 in the 53-note series. Bottom right: D#+11, which refers to the cents notation system: eleven cents higher than the 12-eq D#. Also, 316, which is to say 316 cents above the central C (C is C-6, C to D# is 300 cents above C in 12-eq, and E1b is just under 11 cents above 12-eq C; E’b is also 14 cents above the Eb in 12-eq).
There are all kinds of patterns in the WWMW that you get used to as you work with it. For example, let’s see how easy it is to figure out how to change keys in any scale. We’ll use the example of the Just Mixolydian scale, seven notes which look like this in C:
A1 – E1
| |
F — C — G – D
. |
. B1b
Let’s say you modulate from C Mixolydian to A1 Mixolydian. You would still have two notes on the top rank above the home note, four perfect fifths on the line of the new home key of A1, and one note along the bottom rank. It would have exactly the same shape, like this:
F2# — C2#
| |
D1 – A1 — E1 – B1
. |
. G
Same shape on the WWMW. Easy! Also, notice that C and A1 Just Mixolydian have A1, E1 and G in common. (Hint – those would be good notes to pivot around in such a modulation!). Knowing the shape of C Mixolydian on the WWMW, you can create that same scale in whatever key you are in by simply preserving that mode’s shape. Here’s A3bb Mixolydian, for example:
F2b – C2b
| |
D3bb—A3bb—E3bb—B3bb
. |
. G4bb
On my honeycombed generalized keyboard, the hexagonal black and white keys are all the same shape and distance from one another, so, as it happens, every scale has the same “shape” on the keyboard as well, if the colors of the keys are ignored.
The C Mixolydian mode can also be expressed as a series of fifths, as Pythagoras and the Catholic Church defined it:
Bb – F – C – G –D –A — E
So the shape of a Pythagorean Mixolydian mode will always be the same straight line with a fifth and two fifths below the starting point of the scale. Whatever the 3-limit or 5-limit scale or mode, it is always defined by its shape on the WWMW.
The same is true of chords. Every chord is defined by its intervals. For example, the C Maj7 chord is always a square, looking like this no matter where you start:
E1 – B1
| |
C — G
You can create unnamed tone clusters. Very generally, a tone cluster makes a kind of harmonic sense when the notes are somewhat close to one another, like this:
G2# — D2#
. | — |
. | — F1#
. C
There are patterns everywhere. Find all the “Pythagorean” commas by going up from, say, C twelve fifths to B# (or 12 perfect fifths above any note in the circles and a different pitch in 53-eq); start at C and go up four fifths and down a third to find C1, the same distance to C2, etc.
Using the WWMW, you can also discover how all 53 notes relate to one another harmonically. Starting from the note C, you can create what I call the “Miracle Mode,” first developed by Alain Danielou (see Figure 2-21 in Chapter Two). And yes, the “Miracle Mode” is modulatable, just by starting on any other note you want, and creating the same matchstick structure. Because we are dealing with such a close approximation of Just Intonation, it is for composers of the near future (like you) to discover how far you can take the audience’s ears on a journey through as many of these 53 relationships as newly attuned ears can hear.
Now you can begin to see how 12-eq compares with just intonation. Since every perfect fifth in 12-eq is 2 cents away from a pure perfect fifth, if you start at the note A0 (A-440) and go down by fifths, you get D-2, G-4, C-6, etc. The major thirds are a little over 14 cents off in 12-eq (that’s very bad!), so go up the spine from C and you get C-6, E-21, G#-36, B+49, etc. (in cents notation, when you are more than fifty cents away you just go up or down to the next note and express it that way; there is no such thing as B#-51, for example).
What about the seventh harmonic relationships? To diagram these, you would need a three-dimensional lattice: the horizontal dimension for 3-limit, the vertical dimension for 5-limit, and then a 53-story skyscraper where each “floor” is a five-limit lattice stacked septimally atop one another. In 53-eq, the seventh harmonic is about 4.5 cents off from the nearest note in the 53-eq system. Starting from C, the closest note in 53-eq is A2#. However, to create a seventh chord in common practice tradition, you need the notes C-E-G-B (with flats, double flats and naturals as needed depending on the chord). So we need some kind of C-E-G-Bb. Take the pitch of A2# (two diagonal ascents from C) and find its enharmonic equivalent a skhisma away and you get B1b. So it would look something like this (and of course this can be moved to any other starting point in the circle):
. — — A2#/B1b
|
E1
|
C — G
We will talk more about the seventh harmonic in a later chapter. For now, suffice it to say that the Helmholtz notational system, which works so well to describe the 3-limit and 5-limit notes, creates but an approximation of the true seventh harmonic notes. Since the WWMW is only two-dimensional and you need a third dimension for the seventh harmonic relationships, the 5-limit notational system we are borrowing from Helmholtz necessarily distorts the septimal notation. We have the notes C, D, E, F, G, A and B for one-dimensional 3-limit Pythagorean notation. Helmholtz adds the superscripts and subscripts 1, 2, 3 etc. for 5-limit notation. For the septimal approximations in 53-eq, I don’t add any special notation; I simply use the notations to tell the performer what pitch to play. This is a compromise; the Just Intonation purists do have special notation for septimally generated notes. And by the way, what you see above is a septimal seventh chord. It “looks” like a dominant seventh chord, and can function as a dominant seventh chord. But in fact, it is free of dissonance and sounds more stable than a major triad in 12-eq! So it can stand alone with no real need to “resolve” to an F chord as it would in 12-eq. This is probably the kind of flat seventh chord jazz musicians employ, the kind that needs no resolution. Here are the other three possible nonseptimal patterns of C-E-G-Bb in 53-eq, all of which have overtonal tensions that need resolving:
. E1 E1
. | |
Bb — — C – G C – G – Bb — — C — G — — — E (Pythagorean)
. |
. B1b
For the higher harmonics that are being explored by Johnny Reinhard and many other Just Intonation pioneers of the twentieth and twenty-first centuries, the 53-eq approximations vary by overtone (see Chapter Two). To try to create these approximations in 53-eq using the WWMW, you will once again end up with an enharmonic approximation both notationally and pitch-wise.
But for 3-limit, 5-limit or 7-limit music, you can see that 53-eq offers many more options for you as a composer than the old 12-eq system. Over and over you will find that you are presented with musical choices you never had in 12-eq. And the WWMW is a diagram that actually makes it easy to navigate these waters. Pattern after pattern reveals itself as you go through the WWMW. What I love about this template is the ease with which any scale or mode from anywhere in the world can be understood. You can diagram any ancient scale, compare it to any other ancient scale from anywhere else on the planet, and let them dance together. You can modulate to 53 different keys per scale/mode at will. It would take thousands of composers hundreds of years to exhaust the musical possibilities of 53-eq. So next let’s look more carefully at the pitches of 53-eq and how to notate them in 53-eq.
If you would like to learn more about 53-equal music, you can buy the entire book, The Grand Unified Theory of Music, in pdf form for $25 with hundreds of embedded musical examples of scales and chords from all over the world.
A free introduction to what The Grand Unified Theory of Music offers is on this website and includes both text and a few musical examples from each webpage. If you would like to learn more about this chapter and the full contents of this entire e-book, you can buy The Grand Unified Theory of Music for $25, with hundreds of embedded musical examples of scales and chords from all over the world — and ideas for how to set up your computer system —
HERE.
You’ll get a personalized password you can use to see the entire e-book. Inside the full book, you will also get a link to the complete pdf file of this e-book, which you can read on your Kindle or similar device. The links to the hundreds of mp3 sound files – the same ones you can hear on the website — will also be included. This is “Version 1.0” of The Grand Unified Theory of Music. Because it is an e-book, additions, corrections and improvements in the sound may be added at any time. The Grand Unified Theory of Music is Copyright © 2018 by Christopher Mohr. All rights reserved.
One person per password. Sharing this password with others is a violation of copyright. Do not allow others to use your password or link to the pdf file!