Next Page: 12/4 – Monophony and Polyphony
Mathieu’s Magic Mode
So the question is, how far can we go from the center and still be able to hear a harmonic relationship? When does the noise or obscurity in the outlying realms of harmony blot out the harmony itself? Allaudin Mathieu asserts that the “Magic Mode” (see Harmonic Experience, page 237) allows the twelve notes of the keyboard to represent 31 different Just Intonation pitches. Here is his lattice of Just Intonation notes that can be evoked in 12-eq tuning:
Figure 12-1: All the enharmonic notes from C in 12-eq
. F2# — C2# — G2# — D2#
. | | | |
. D1 — A1 — E1 — B1 — F1# — C1#
. | | | | | |
Db – Ab – Eb – Bb — F — C — G — D — A – E – B – F#
. | | | | | |
. G1b – D1b – A1b – E1b — B1b — F1
The 28 notes above are thirds and fifths away from our central note C. Allaudin Mathieu adds several “blu” notes, which evoke Seventh-Harmonic relationships: C2#, D2#, G2# and A2#. As we just discovered in the last chapter, in 53-eq, that top row of pitches two Just Thirds above the C spine of fifths creates several 53-eq “commas” between the Third-of-Third pitches and the Seventh-Harmonic pitches. So with the 12-eq palette, we need only add the A2# to the list above to get all the Blu notes Allaudin’s 12-eq system allows for. The nearest 12-eq pitches are almost a quarter-tone sharp from the just sevenths, but skillful musicians (especially in jazz and blues) evoke it all the time, and of course vocalists often sing the Just Sevenths in tune in spite of the instrumentalists.
In 53-eq, can you travel even further afield and still have a musically meaningful relationship with your dronal note(s)? I think the answer is yes, but it will take much more experimentation to find those aural limits. Considering that the history of music is in part a history of expanding our musical sensibilities to embrace more and more complex harmonic relationships, I believe that 53-eq will allow composers to push the boundary between music and noise considerably further. That’s because there is much less “noise” in 53-eq. When two notes are in almost-perfect pitch alignment, you can hear the relationship between them, almost no matter how obscure.
So how far can we go? On the horizontal C spine, I don’t think we can go any further, because we already have the twelve notes of a Pythagorean chromatic scale. Go any further and you bump against the Pythagorean comma, which gets us into the realm of musical confusion and harmonic conflict. I also doubt that you can go any further up by Just Thirds. If you go higher on Ga spine, you bump into the Great Diesis (three Just Thirds up from C is B3#, 41 cents flatter than C). That too creates musical confusion when you are sticking to your dronal note. It’s fine if you make a key or chord change, of course, but for now we are talking about notes that can be sounded simultaneously with C and have any harmonic/auditory relationship . Even without the unpleasant sound of the Great Diesis, three Just Third leaps may be an awfully big stretch for the ear. I believe you can go down by two Major Thirds as long as you don’t wander too far on the horizontal Pythagorean axis at the same time. I also believe you can go further across on each spine.
Still, when I try to sing these more distant intervals from C, I can’t really pull it off. It seems that Allaudin Mathieu’s “Magic Mode” is a pretty good representation of what can be sung using only a drone and your own voice and ear. Mathieu might say, if ya can’t sing it, it ain’t real. And there is certainly the danger of just plugging complex ratios into your computer and calling it music. Some of Xenakis’s 20th century theoretical principles evolved from his knowledge of architecture, and I for one never cared for the music he wrote based on that concept. The same can apply for obscure musical tunings. But maybe the ear can hear more than the voice can replicate. In my compositions I sometimes stretch a bit beyond my teacher’s “Magic Mode,” and consider these intervals (plus a whole bunch of seventh harmonic intervals we’ll talk about later) to be at the new frontier of the recognizable. 53-eq certainly boosts the signal-to-noise ratio! Here is a possible Extended Magic Mode, adding in red the notes most people cannot sing but perhaps can hear:
Figure 12-2: Notes the ear can hear in relation to C in 53-eq
. B2 — F2# — C2# — G2# –D2# — A2# — E2#
. | | | | | | |
. G1 — D1 — A1 — E1 — B1 — F1# — C1# — G1#
. | | | | | | | |
Db – Ab – Eb – Bb — F — C — G — D — A – E – B – F#
. | | | | | | |
. C1b — G1b – D1b – A1b – E1b — B1b — F1
. . | | |
. B2bb — F2b – C2b
The B2, A2# and E2# that I’ve added to the top row of potential sonic relationships to C are there because they can represent various seventh-harmonic intervals. I have serious doubts about the G1 in the second row down, because of its proximity to the dronal G. For starters, the G1 is a “wolf interval” from C. I doubt that it can be heard as anything but a wretchedly out-of-tune dominant as long as the C is being intoned at the same time. The primary third-harmonic relationship of C to G trumps any fancy harmonic ideas you may be trying to get across. I didn’t include the C1 at all (it would be just to the left of G1 on our little lattice map), or for that matter the C1 (which would be just to the right of F1) because, well, either would be an out-of-tune tonic. Michael Harrison would disagree with me, as he calls for “the liberation of the comma” in music (Michael Harrison, Revelation: Music for the Harmonically Tuned Piano, MHM101). He believes that from 1100 A.D., when the major third was rejected as a dissonance, through the eras of 1450-1900 when thirds and then seconds and sevenths were allowed, to Schoenberg’s “liberation of dissonance” in 12-tone music, to his “comma-liberated” music where even microtonal intervals can be played at the same time or as trills and other decorative effects, is a natural progression. Philip Glass loves Harrison’s Seven-Limit, Just-Intonation, comma-emphasizing minimalistic 12-note piano music. “Liberating the comma” sounds to me like the aural equivalent of freeing violent prisoners en masse. I played Harrison’s music without any introduction for one of my friends, and he started literally screaming! Others love it, and say it creates a shimmering sonic texture never before heard. He is indeed right that commas and “wolf intervals” have historically been a problem to deal with and not a tool to exploit in a composer’s bag of tricks. I reject his esthetic, but hey, nothing I say can stop you from picking up on Michael Harrison’s ideas and liberating comma after comma while your humble author howls at the moon. 53-eq is a template, not an aesthetic.
We’ve also talked about the representation of higher harmonics in 53-eq. Since the 11th harmonic is less in-tune than the third, fifth or seventh harmonics, and the soft volume of this harmonic makes it hard to hear even when it’s perfectly in tune, I choose not to explore it in 53-eq. If you really want to explore these harmonics in your music, I think you are a better candidate for pure Just Intonation as your tuning template.
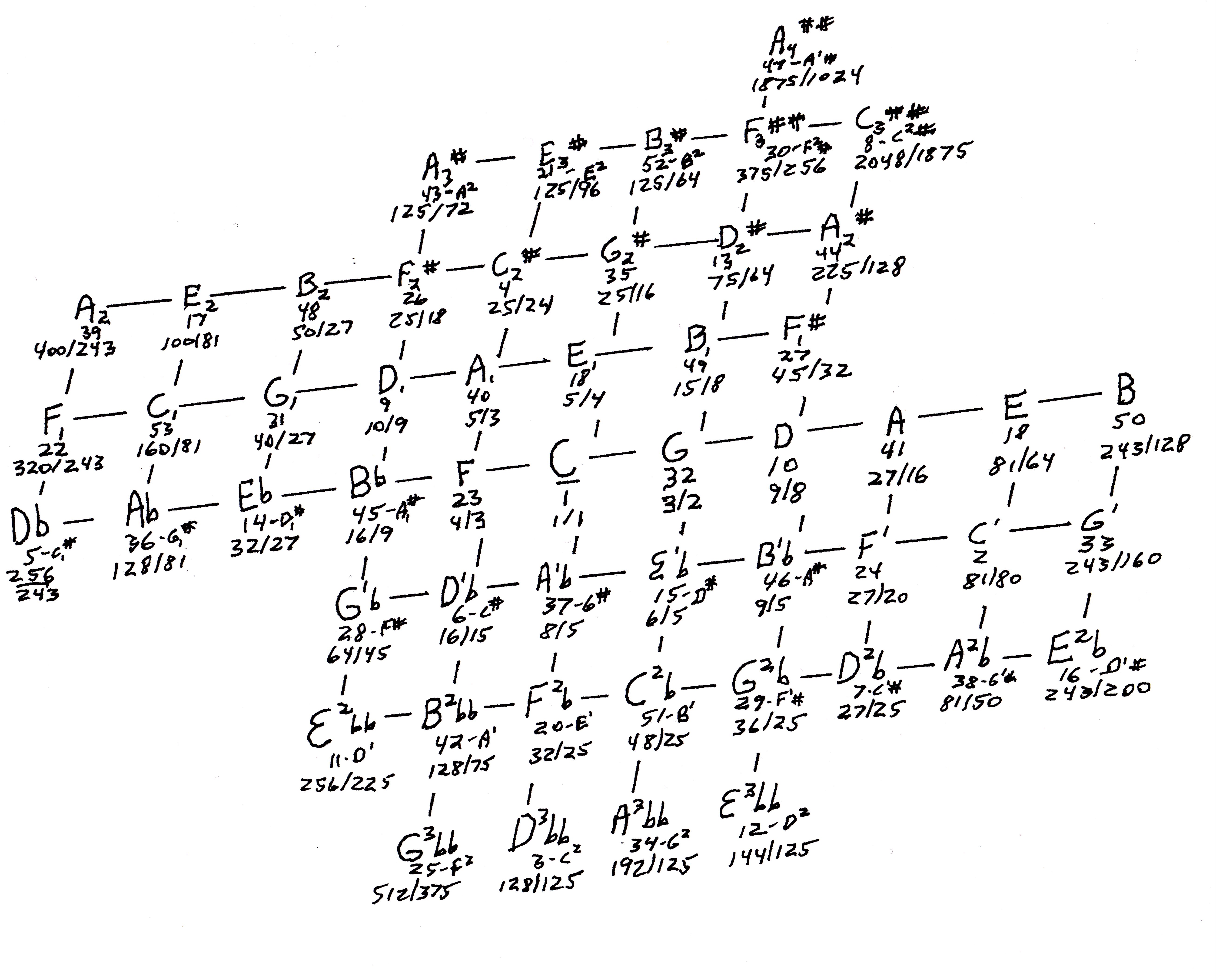
My Extended Magic Mode (above) may not be the actual boundary of audible harmonic relationships. Alain Danielou, in Music and the Power of Sound, has suggested that every note in the 53-eq palette has harmonic meaning which can be heard by the ear. Translating his thoughts into our familiar lattice map, he shows the ratios and harmonic pathways of all 53 notes from C. When I first encountered this, I called it “The Miracle Mode,” to show that it’s the next order up from Mathieu’s “Magic Mode.” But frankly, some of the extreme outlying harmonic relationships in the “Miracle Mode” are too obscure for my ears to grok. The only way such a distant note relates to the drone C in my ear is the vague sense that the harmonic relationship is very obscure but not actually dissonant, at least not in the way we hear true dissonance everywhere in 12-eq. In other words, perhaps there is some audible relationship there, just too remote for me to grasp. I’m keeping the “Miracle Mode” name for a new reason: it would be a miracle if anyone could actually make sense of these distant harmonies! It’s certainly very interesting that every single pitch in 53-eq is very close to a pure Just ratio from every other pitch.
Figure 12-3: Miracle Mode, 53 Danielou file
Chord Progressions: Pulling Up the Anchor
*Simple*
We have already talked about the possibility of employing chord progressions over a drone (usually tonic or dominant). Bach and others did it all the time, if only for short periods. You can create some rich sounds when you play the C drone and then play chords that don’t have C within their triads. The drone keeps you directly centered aurally as you wander about. It’s a great way to explore the outer reaches of 53-eq harmonic relationships, like a 1-year-old wandering around but always within earshot of Mom. You can start with the notes harmonically more closely related, wander off into some exciting new corners of the Miracle Mode lattice, then come back home. It’s a little like being on a boat, anchored but being moved about by the waves.
We see the abandonment of dronal music in the West as far back as Gregorian Chant, where the tonic is assumed by the melody, and the drone is completely absent. By the Middle Ages, composers of organum often wrote music that sounded dronal, except that the bass tone would move periodically. Each move of the bass in this neo-dronal era feels like a real shift in the musical energy. Indeed, it is a paradigm shift of vast proportions, which many cultures never took on. As we have said, the drone was the center of the universe, the Abiding Self, the imperishable Om. In India, moving the drone is like destroying and recreating the entire universe.
It wasn’t until the 1500s that chords began to play an important role in Western music. By the 1600s, composers felt free to “pull anchor” and take harmonic journeys via chord progressions that inevitably started and ended on the tonic. By this time, dronal music was almost nonexistent, echoed only in the occasional pedal tones of Bach and other Masters. Perhaps the drone was symbolized by the fact that the music started and ended in the tonic. It’s there, the composer promises, and I’ll help you find it again.
If you would like to learn more about this chapter, “Mathieu’s Magic Mode,” and much more, you can buy the entire book, The Grand Unified Theory of Music, in pdf form for $25 with hundreds of embedded musical examples of scales and chords from all over the world.
A free introduction to what The Grand Unified Theory of Music offers is on this website and includes both text and a few musical examples from each webpage. If you would like to learn more about this chapter and the full contents of this entire e-book, you can buy The Grand Unified Theory of Music for $25, with hundreds of embedded musical examples of scales and chords from all over the world — and ideas for how to set up your computer system —
HERE.
You’ll get a personalized password you can use to see the entire e-book. Inside the full book, you will also get a link to the complete pdf file of this e-book, which you can read on your Kindle or similar device. The links to the hundreds of mp3 sound files – the same ones you can hear on the website — will also be included. This is “Version 1.0” of The Grand Unified Theory of Music. Because it is an e-book, additions, corrections and improvements in the sound may be added at any time. The Grand Unified Theory of Music is Copyright © 2018 by Christopher Mohr. All rights reserved.
One person per password. Sharing this password with others is a violation of copyright. Do not allow others to use your password or link to the pdf file!