Next Page: 2/9 Journey Away From Eden
*Advanced*
Commas and Meantone Temperaments
As music became more complex and fixed-pitch keyboard instruments like the organ more common, certain harmonic clashes became harder and harder to sidestep. We have already mentioned the Pythagorean comma (12 perfect fifths from C to B# leaving a 23.46 cent gap), a comma which rarely is an issue because few composers traverse all twelve key signatures of the circle of fifths in a single work. We also discussed the much more common problem of the Didymic comma (when you go four fifths up and one third down, you get a 21.5-cent difference between, say the D and the D1 relative to C). To which D do you tune your instrument? Whichever D you choose, in just intonation you’ll soon be playing one of them badly out-of-tune as you move about harmonically on a 12-note keyboard! Another comma, the Great Diesis, is created when you travel up by three major thirds. From C to E1 to G2# to B3# leaves a 41-cent gap between your B# and your C in just intonation. There is also the Diaschisma (four fifths down and two major thirds down) which creates a “comma,” or tuning gap, of 19.5 cents. Figure 2-11 shows color-coded examples of all these commas. By the way, it’s worth noting that each step in a 53-equally-tuned octave is 22.6415 cents, which is to say that none of these 12-eq commas exist in 53-equal tuning: you are always playing one note or the other when two notes come close together in pitch. The size of most commas is very close to either one or two steps in 53-eq. I use the term “generic comma” to refer to the 22.6415 cents distance from one pitch to the next in 53-eq, since it so closely approximates the commas (or two “generic commas” in the case of the Great Diesis and zero “generic commas for the Skhisma).
Figure 2-11: the comma problem in 12-notes-to-the-octave keyboards and frets, color-coded
Great Diesis: C to B3# 41 cents B3# Pythagorean Comma C to B# 23.46 cents
. . | Didymic Comma D to D1 21.5 cents
. . G2# Diaschisma F1# to G1b 19.5 cents
. . | Skhisma Bb to A1# 2 cents (same note in 53)
. . D1 – A1 – E1 – B1 – F1#– C1#-G1#-D1#-A1#
. . | | | | | | | | |
. . Bb F – C – G – D – A – E – B – F# – C# – G# – D# – A# – E# – B#
. . |
. . G1b
With the exception of the Skhisma (a 2-cent comma), these commas on a just-tuned 12-note-to-the-octave keyboard eventually became walls to further harmonic exploration. This is because when you tune your twelve notes to play a D-F-A1 chord in C, for example, you get a truly wretched sound. In Figure 2-12, check out and listen to the D1-F-A1 chord (consonant minor triad) and the D-F-A1 chord and you too will howl like a wolf!
Figure 2-12: D minor chord without and then with “wolf” fifth
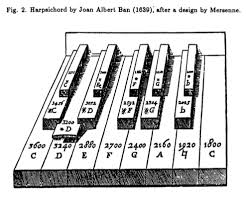
One solution is to create instruments with more keys or frets, to play both the D and the D1, for example. This has been attempted many times, as you can see in Figure 2-13. Most of these keyboards had 20-24 keys per octave, but in 1640 Nicholas Ramarinus actually constructed the world’s first 53-note-to-the-octave keyboard. Most keyboardists said that 12 keys in an octave was enough, thank you, and resisted these other instruments due to the performance difficulties. The instruments themselves were also much bulkier, requiring extra strings and heavier sounding boards.
Figure 2-13: keyboards with more than 12 notes in an octave
The solution executed in 1496 by Arnold Schlick and Henricus Grammateus was to leave musical Eden. Because ears accustomed to just intonation would want to hear the ancient harmonic purity as much as possible, a series of subtle compromises was created in various meantone temperaments. What if the D on the keyboard could play both D’s by compromising the pitch of each just a bit? The goal of meantone temperament was to create several keys with very good major thirds, pretty good minor thirds and sixths, slightly flatted fifths in the central keys, and one very bad perfect fifth in the most remote key possible. Of all the different meantone temperaments attempted, the one that came closest to just intonation while employing only twelve keys representing over 20 different notes was “quarter-comma meantone,” which yielded eight good major triads, eight good minor triads, four badly out of tune major triads, and four badly out of tune minor triads. This worked well for a couple centuries, but as music became still more complex (can you spell Bach?), composers exploring more remote key transpositions hit the “wall” of meantone temperament. Musical progress was held back once again. In 1650, Athanasius Kircher advocated yet again for a 53-eq template, but his research was largely ignored.
If you would like to learn more about the 53-equal tuning that embraces all of ancient music, you can buy the entire book, The Grand Unified Theory of Music, in pdf form for $25 with hundreds of embedded musical examples of scales and chords from all over the world.
A free introduction to what The Grand Unified Theory of Music offers is on this website and includes both text and a few musical examples from each webpage. If you would like to learn more about this chapter and the full contents of this entire e-book, you can buy The Grand Unified Theory of Music for $25, with hundreds of embedded musical examples of scales and chords from all over the world — and ideas for how to set up your computer system —
HERE.
You’ll get a personalized password you can use to see the entire e-book. Inside the full book, you will also get a link to the complete pdf file of this e-book, which you can read on your Kindle or similar device. The links to the hundreds of mp3 sound files – the same ones you can hear on the website — will also be included. This is “Version 1.0” of The Grand Unified Theory of Music. Because it is an e-book, additions, corrections and improvements in the sound may be added at any time. The Grand Unified Theory of Music is Copyright © 2018 by Christopher Mohr. All rights reserved.
One person per password. Sharing this password with others is a violation of copyright. Do not allow others to use your password or link to the pdf file!